My first article: A not fully crossed design

Statistical analyses for my first article published

Marie Vaugoyeau

7 minutes read

In 2015, I published the article: Is oxidative status influenced by dietary carotenoid and physical activity after moult in the great tit (Parus major)? about my first experimentation. In the aim to investigate on the relationship between dietary carotenoids, physical activity and oxidative status, I captured great tits and kept them in aviaries.
Initially, a cross design: with/without dietary carotenoids and with/without plucking primary feathers (to increase physical activity or not), was planned. Due to weather conditions, number of caught birds was to low to do it, so only three treatments were done.

Table 1: Expected crossed design
Dietary carotenoids in water Natural water
Physical activity increased 7F 7M 7F 7M
Normal physical activity 7F 7M 7F 7M

With F = females and M = males

Unfortunately, I caught only 42 adults (1 was dead before the beginning of the experiment).

Table 2: Real crossed design
Dietary carotenoids in water Natural water
Physical activity increased 6F 8M 5F 8M
Normal physical activity 7F 7M

Here I detail the statistical analyses that I did it.

First Step: Check the repeatability of the data

For some characteristics (counts heterophiles on lymphocytes, feathers colour…), I did two, three or four measurements. To measure repeatability, I used a linear model which give me F-statistic with freedom degree and p-value.

mod<-lm(Area~Identity, data=X)
anova(mod)
## Analysis of Variance Table
## 
## Response: Area
##            Df  Sum Sq Mean Sq F value   Pr(>F)   
## Identity    1  11.558 11.5584  10.346 0.001655 **
## Residuals 124 138.528  1.1172                    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

In this article, I also calculated manually intraclass correlation coefficient according Lessells and Boag’s method 1987: r = (MSA - MSw)/(MSA + MSW(n-1)).

Once repeatability was checked, I calculated and used only means.

Second step: Linear mixed models with backward elimination

In order to test the effects of physical activity and dietary carotenoid availability on the antioxidant system (total antioxidant capacity, ROM concentration, total carotenoids, vitamin A and vitamin E), on the stress response (blood sedimentation and H/Ly ratio) and on plumage colour (lutein absorbance, carotenoid chroma and UV brightness), all models included as fixed effects tarsus length and body mass, and three-way interactions among carotenoid supplementation or physical handicap with sex and time of experiment (start or end of the experiment).

Linear mixed model

For each variable, I write a mixed model like that:

library(nlme)
m1<-lme(Oxy ~ Tarsus+Mass+Exp*Sex*Carot+Exp*Sex*Plucking, random=list(Aviary=~1, Identity=~1), method="ML", data = Y, na.action=na.exclude)

To consider biological variance, aviaries and individual identity were included as random factors.

Distribution of model residuals

To validate a posteriori the used of linear model, I tested residuals distribution with Shapiro test and Q-Q plot.

shapiro.test(residuals(m1))
## 
##  Shapiro-Wilk normality test
## 
## data:  residuals(m1)
## W = 0.98678, p-value = 0.5759
qqnorm(residuals(m1));qqline(residuals(m1))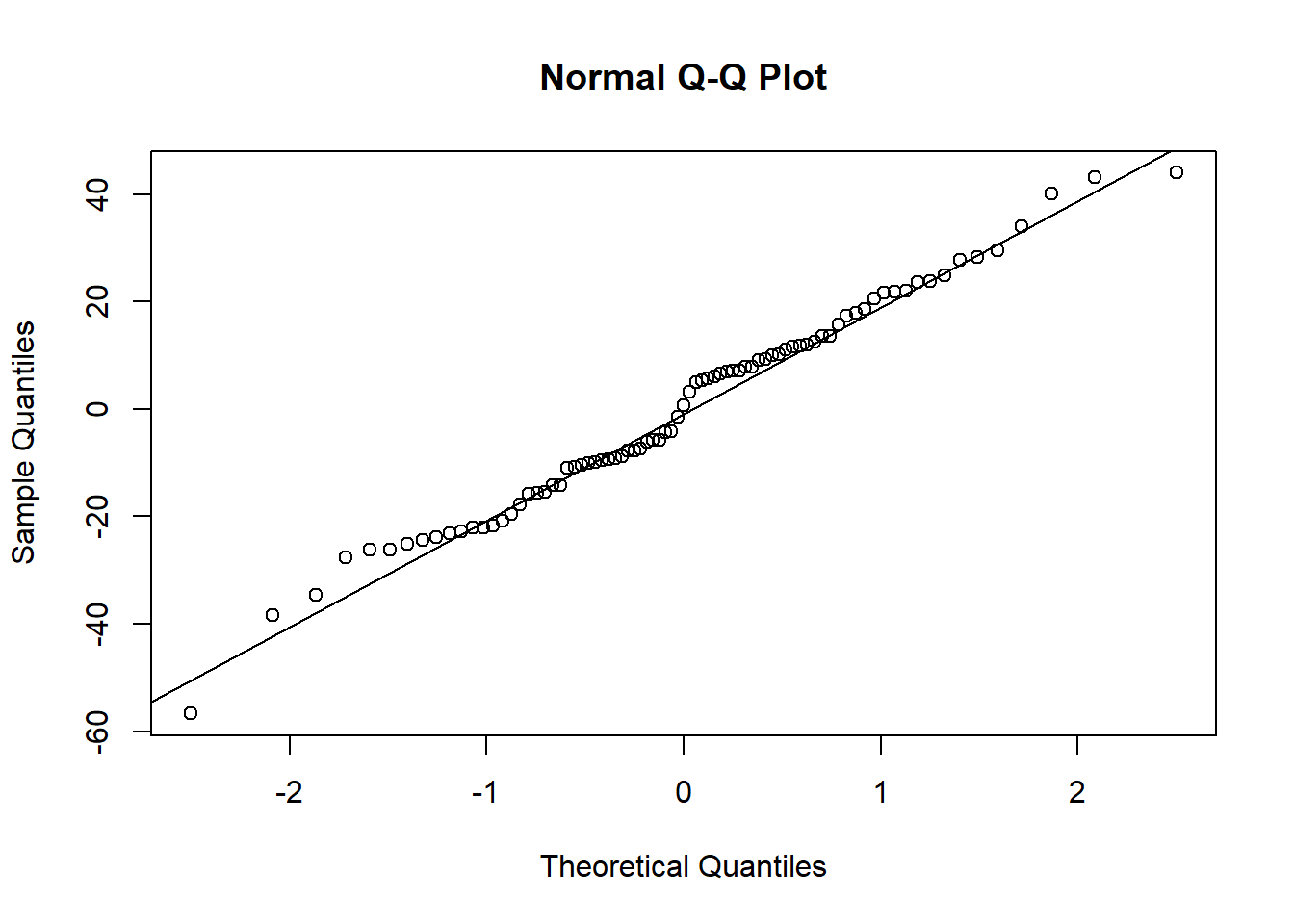

If residuals did not follow normal distribution, variable was log-transformed.

Model selection with backward elimination

About first model, I created a new one by removing one fixed factor. Then, I used Akaike’s Information Criterion to select the best predictive model between both.

anova(m1)
##                  numDF denDF  F-value p-value
## (Intercept)          1    33 3894.578  <.0001
## Tarsus               1    25    9.314  0.0053
## Mass                 1    33    0.414  0.5243
## Exp                  1    33   37.679  <.0001
## Sex                  1    25    5.208  0.0313
## Carot                1     9    0.519  0.4897
## Plucking             1     9    1.001  0.3432
## Exp:Sex              1    33    0.888  0.3529
## Exp:Carot            1    33    2.560  0.1191
## Sex:Carot            1    25    0.017  0.8986
## Exp:Plucking         1    33    1.918  0.1753
## Sex:Plucking         1    25    2.002  0.1694
## Exp:Sex:Carot        1    33    0.113  0.7391
## Exp:Sex:Plucking     1    33    0.782  0.3831
summary(m1)
## Linear mixed-effects model fit by maximum likelihood
##  Data: Y 
##        AIC      BIC    logLik
##   772.4558 813.1614 -369.2279
## 
## Random effects:
##  Formula: ~1 | Aviary
##         (Intercept)
## StdDev:     7.01982
## 
##  Formula: ~1 | Identity %in% Aviary
##         (Intercept) Residual
## StdDev:    7.071078 21.21047
## 
## Fixed effects: Oxy ~ Tarsus + Mass + Exp * Sex * Carot + Exp * Sex * Plucking 
##                               Value Std.Error DF   t-value p-value
## (Intercept)               289.61059 143.81205 33  2.013813  0.0522
## Tarsus                     -3.63000   6.48630 25 -0.559640  0.5807
## Mass                       -0.09082   4.43841 33 -0.020462  0.9838
## ExpStart                   44.13499  13.03342 33  3.386293  0.0018
## SexM                      -14.94850  15.46285 25 -0.966736  0.3429
## CarotYes                   -1.46163  16.34930  9 -0.089400  0.9307
## PluckingYes                23.53261  15.67578  9  1.501208  0.1675
## ExpStart:SexM               5.54477  18.34549 33  0.302241  0.7644
## ExpStart:CarotYes         -11.31881  19.99812 33 -0.565994  0.5752
## SexM:CarotYes              10.80621  20.00440 25  0.540192  0.5938
## ExpStart:PluckingYes       -5.26320  19.44272 33 -0.270703  0.7883
## SexM:PluckingYes           -9.06389  20.22299 25 -0.448197  0.6579
## ExpStart:SexM:CarotYes      4.51084  25.90055 33  0.174160  0.8628
## ExpStart:SexM:PluckingYes -23.19101  26.23251 33 -0.884056  0.3831
##  Correlation: 
##                           (Intr) Tarsus Mass   ExpStr SexM   CartYs PlcknY
## Tarsus                    -0.873                                          
## Mass                      -0.247 -0.251                                   
## ExpStart                   0.031  0.073 -0.292                            
## SexM                       0.283 -0.133 -0.381  0.497                     
## CarotYes                   0.042 -0.144  0.205 -0.060 -0.056              
## PluckingYes               -0.168  0.147 -0.050  0.395  0.353 -0.558       
## ExpStart:SexM             -0.005 -0.056  0.182 -0.703 -0.662  0.038 -0.279
## ExpStart:CarotYes          0.013  0.013 -0.052  0.015  0.020 -0.621  0.350
## SexM:CarotYes              0.064  0.047 -0.222  0.065  0.087 -0.732  0.402
## ExpStart:PluckingYes      -0.001 -0.029  0.116 -0.647 -0.303  0.366 -0.618
## SexM:PluckingYes           0.075 -0.131  0.175 -0.346 -0.656  0.417 -0.690
## ExpStart:SexM:CarotYes    -0.002 -0.002  0.008 -0.002 -0.003  0.473 -0.268
## ExpStart:SexM:PluckingYes  0.001  0.036 -0.115  0.488  0.458 -0.278  0.459
##                           ExS:SM ExS:CY SxM:CY ExS:PY SxM:PY ES:SM:C
## Tarsus                                                              
## Mass                                                                
## ExpStart                                                            
## SexM                                                                
## CarotYes                                                            
## PluckingYes                                                         
## ExpStart:SexM                                                       
## ExpStart:CarotYes         -0.009                                    
## SexM:CarotYes             -0.040  0.510                             
## ExpStart:PluckingYes       0.457 -0.566 -0.305                      
## SexM:PluckingYes           0.488 -0.278 -0.537  0.495               
## ExpStart:SexM:CarotYes     0.001 -0.770 -0.649  0.433  0.339        
## ExpStart:SexM:PluckingYes -0.697  0.421  0.362 -0.745 -0.672 -0.521 
## 
## Standardized Within-Group Residuals:
##         Min          Q1         Med          Q3         Max 
## -2.67403721 -0.67266044  0.03448938  0.58915181  2.07277186 
## 
## Number of Observations: 81
## Number of Groups: 
##               Aviary Identity %in% Aviary 
##                   12                   41
m2<-lme(Oxy ~ Tarsus+Mass+Exp*Carot+Sex*Carot+Exp*Sex*Plucking, random=list(Aviary=~1, Identity=~1), method="ML", data = Y, na.action=na.exclude)
anova(m1,m2)
##    Model df      AIC      BIC    logLik   Test    L.Ratio p-value
## m1     1 17 772.4558 813.1614 -369.2279                          
## m2     2 16 770.4925 808.8036 -369.2462 1 vs 2 0.03665401  0.8482

I kept the model with the smaller AIC or if difference between AIC was smaller than 2, the most parsimonious.

Final model

Final models were maximum-likelihood (REML) linear mixed models, run using the same function lme and the function Anova in the package car, with type III sum of squares.

mf<-lme(Oxy ~ Sex+Exp*Plucking, random=list(Aviary=~1, Identity=~1), method="REML", data = Y, na.action=na.exclude)
shapiro.test(residuals(mf))
## 
##  Shapiro-Wilk normality test
## 
## data:  residuals(mf)
## W = 0.99136, p-value = 0.8646
qqnorm(residuals(mf));qqline(residuals(mf))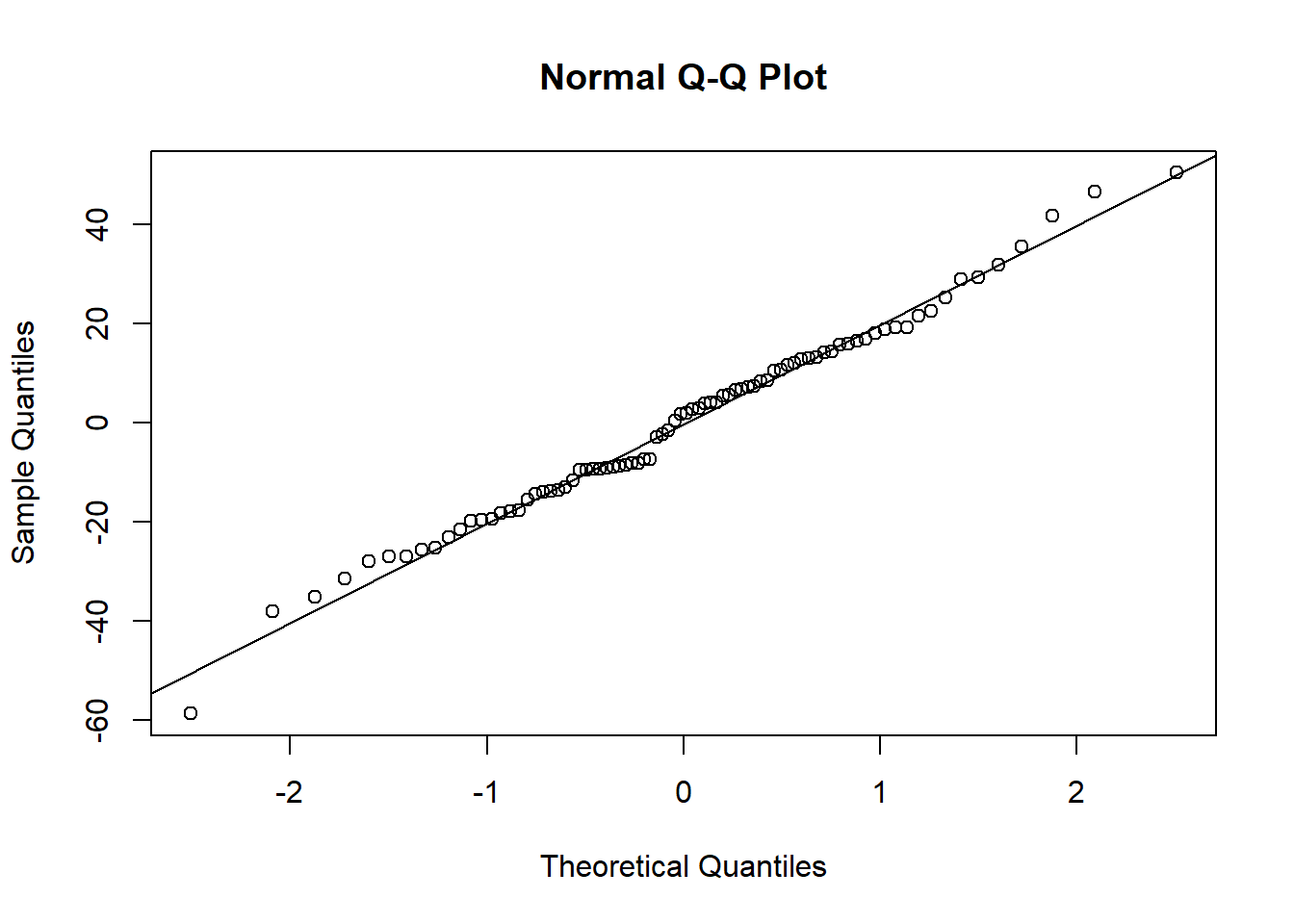

library(car)
Anova(mf, type="III")
## Analysis of Deviance Table (Type III tests)
## 
## Response: Oxy
##                 Chisq Df Pr(>Chisq)    
## (Intercept)  711.1752  1  < 2.2e-16 ***
## Sex           17.7193  1  2.560e-05 ***
## Exp           31.2056  1  2.321e-08 ***
## Plucking       5.6370  1    0.01759 *  
## Exp:Plucking   4.9661  1    0.02585 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
summary(mf)
## Linear mixed-effects model fit by REML
##  Data: Y 
##        AIC      BIC    logLik
##   740.8622 759.6127 -362.4311
## 
## Random effects:
##  Formula: ~1 | Aviary
##         (Intercept)
## StdDev:    7.375749
## 
##  Formula: ~1 | Identity %in% Aviary
##         (Intercept) Residual
## StdDev:    8.367793 22.21293
## 
## Fixed effects: Oxy ~ Sex + Exp * Plucking 
##                          Value Std.Error DF   t-value p-value
## (Intercept)          211.16883  7.918474 39 26.667869  0.0000
## SexM                 -24.19386  5.747544 28 -4.209425  0.0002
## ExpStart              46.90000  8.395700 39  5.586193  0.0000
## PluckingYes           21.58673  9.092049 10  2.374242  0.0390
## ExpStart:PluckingYes -23.05556 10.345869 39 -2.228479  0.0317
##  Correlation: 
##                      (Intr) SexM   ExpStr PlcknY
## SexM                 -0.363                     
## ExpStart             -0.530  0.000              
## PluckingYes          -0.736 -0.054  0.462       
## ExpStart:PluckingYes  0.430  0.000 -0.812 -0.569
## 
## Standardized Within-Group Residuals:
##         Min          Q1         Med          Q3         Max 
## -2.64507717 -0.62459656  0.07843944  0.59250358  2.26879382 
## 
## Number of Observations: 82
## Number of Groups: 
##               Aviary Identity %in% Aviary 
##                   12                   41

Random effect

For all final model, random factors (aviaries and individual identity) were unsignificant. I tested it by the follow way:

mfR<-lme(Oxy ~ Sex+Exp*Plucking, random=list(Aviary=~1, Identity=~1), method="REML", data = Y, na.action=na.exclude)
mfNR<-gls(Oxy ~ Sex+Exp*Plucking, method="REML", data = Y, na.action=na.exclude)
anova(mfR,mfNR)
##      Model df      AIC      BIC    logLik   Test L.Ratio p-value
## mfR      1  8 740.8622 759.6127 -362.4311                       
## mfNR     2  6 739.2564 753.3192 -363.6282 1 vs 2 2.39415  0.3021

Third and last step: Analyse results

The last and a good one at that: analyse results and wrote article.

If you read until here, thank you. I remain at your disposal for questions and comments. If you want a pdf, full text is available here.