Principal Component Analysis
How I do Principal Component Analysis and choice of n factors

With article about correlations, we saw data from airquality were correlated.
Sometimes it is need to use Principal Component Analysis (PCA) to determine non correlated variables in order to analyze data.
It is the subject of this blog article and especially, how many new variables were needed.
PCA
As previously I use airquality as data.
To do PCA, I use the package FactoMineR.
library(FactoMineR)
D<-airquality
pca<-PCA(D)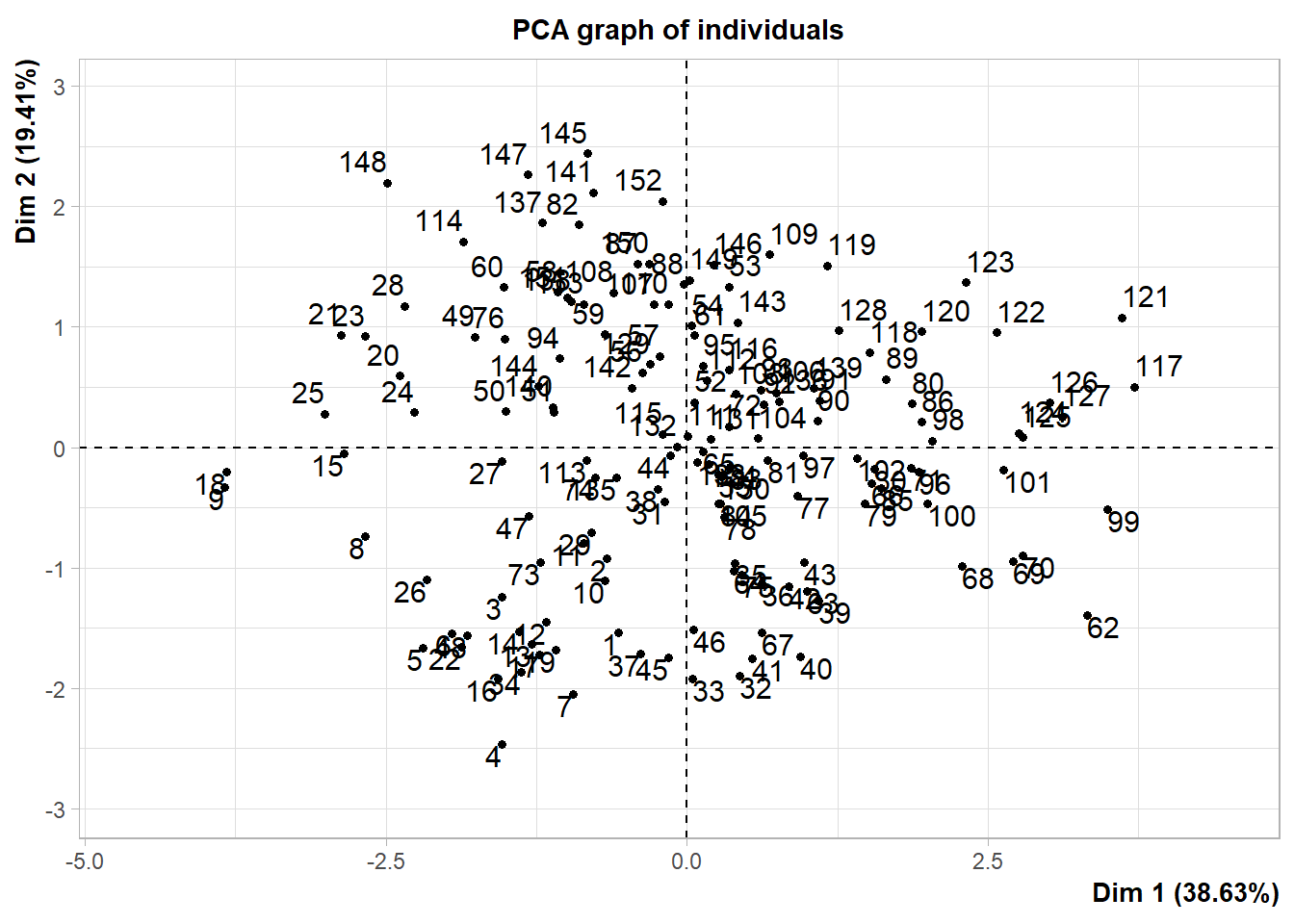
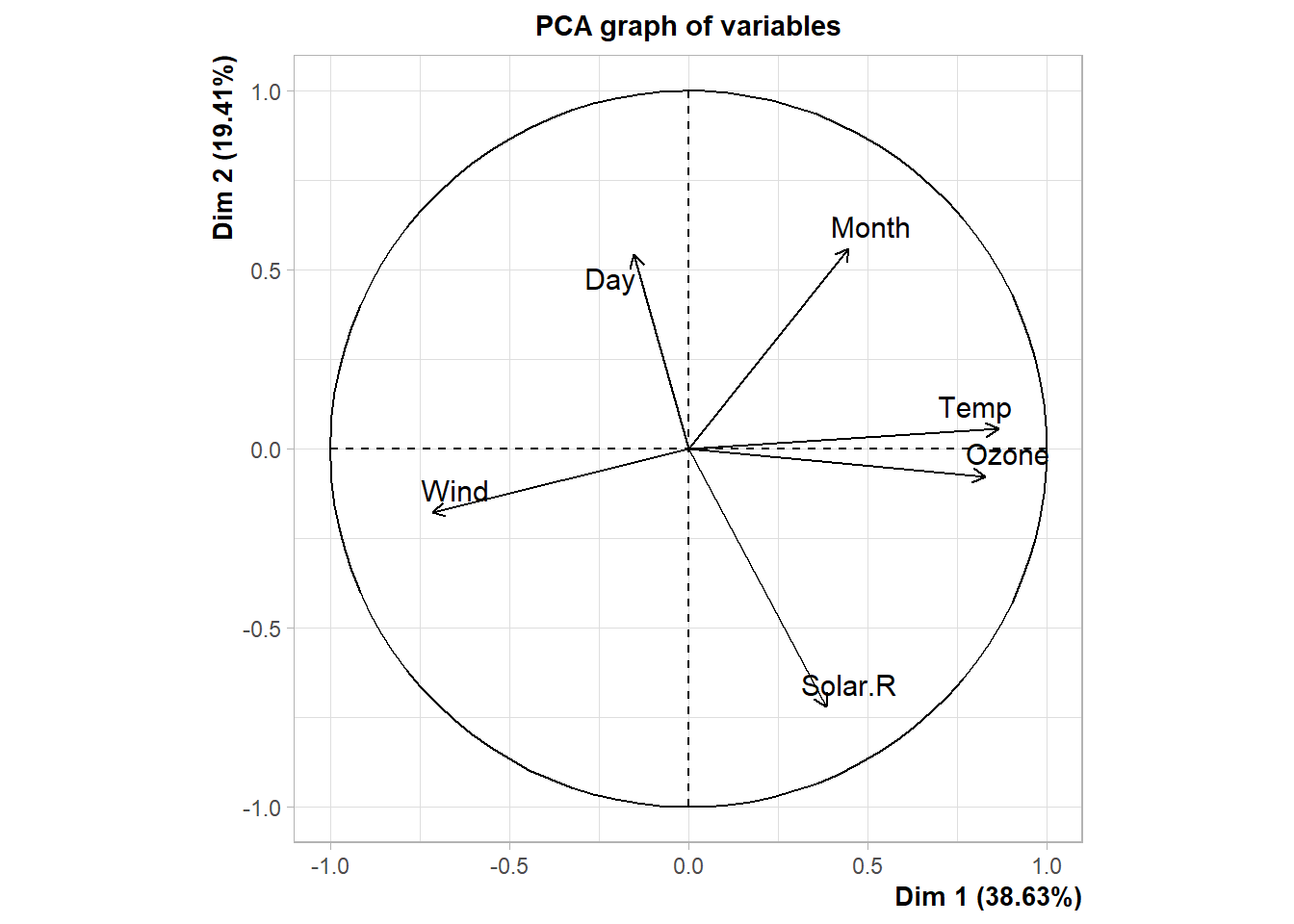
pca$eig## eigenvalue percentage of variance cumulative percentage of variance
## comp 1 2.3175145 38.625242 38.62524
## comp 2 1.1646466 19.410776 58.03602
## comp 3 0.9830994 16.384990 74.42101
## comp 4 0.7904881 13.174802 87.59581
## comp 5 0.4347422 7.245704 94.84151
## comp 6 0.3095092 5.158486 100.00000The question is how much dimensions do we need to keep?
The wonderful package psycho of Dominique Makowski has the response. Thank him!
Updated, the n_factors() function now belongs to the parameters package.
Number of factor retained by psycho::n_factors()
library(magrittr)
library(psycho)
choice <- D %>% parameters::n_factors()
choice## # Method Agreement Procedure:
##
## The choice of 1 dimensions is supported by 5 (33.33%) methods out of 15 (Optimal coordinates, Acceleration factor, SE Scree, TLI, RMSEA).summary(choice)## n_Factors n_Methods
## 1 0 1
## 2 1 5
## 3 2 4
## 4 3 1
## 5 5 3
## 6 6 1plot(choice)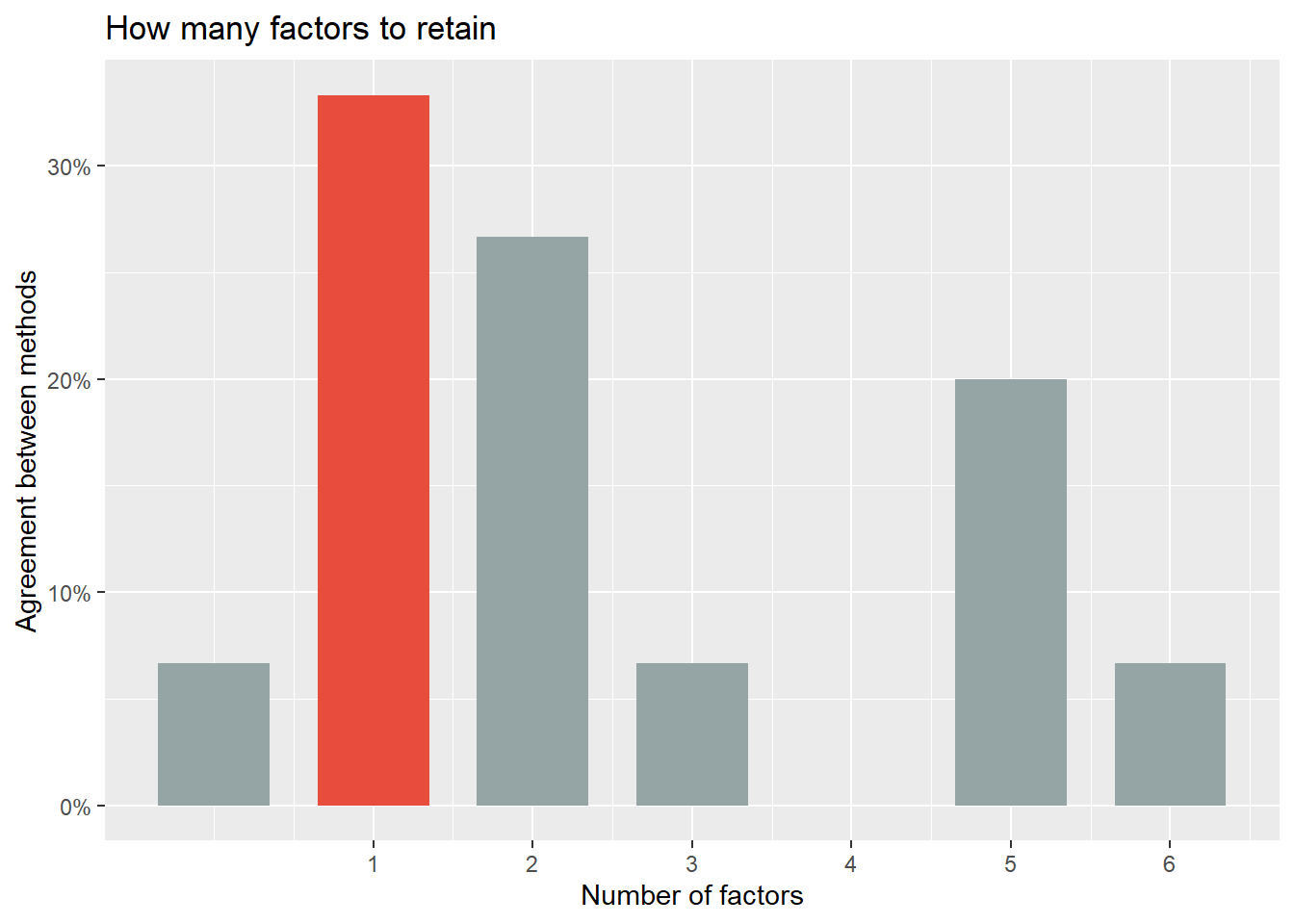
On the plot which shows the summary, you can see in yellow, the number of methods. The red line is the Eigenvalues and the blue line, the cumulative proportion of explained variance.
According to this method, we can keep the two first dimensions from PCA.
Extraction of the variables
dimdesc from FactoMineR gives correlations and p-value.
X is the new data comes from PCA.
dimdesc(pca, axes = 1:2)## $Dim.1
## $quanti
## correlation p.value
## Temp 0.8657470 3.027143e-47
## Ozone 0.8283780 7.735036e-40
## Month 0.4466436 7.164874e-09
## Solar.R 0.3851781 8.816862e-07
## Wind -0.7145176 3.380623e-25
##
## attr(,"class")
## [1] "condes" "list"
##
## $Dim.2
## $quanti
## correlation p.value
## Month 0.5579040 6.798713e-14
## Day 0.5418723 4.714049e-13
## Wind -0.1779546 2.775569e-02
## Solar.R -0.7203875 9.044341e-26
##
## attr(,"class")
## [1] "condes" "list"
##
## $call
## $call$num.var
## [1] 1
##
## $call$proba
## [1] 0.05
##
## $call$weights
## [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
## [38] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
## [75] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
## [112] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
## [149] 1 1 1 1 1
##
## $call$X
## Dim.1 Ozone Solar.R Wind Temp Month Day
## 1 -0.569773734 41.00000 190.0000 7.4 67 5 1
## 2 -0.662866496 36.00000 118.0000 8.0 72 5 2
## 3 -1.535704204 12.00000 149.0000 12.6 74 5 3
## 4 -1.535948761 18.00000 313.0000 11.5 62 5 4
## 5 -2.190872096 42.12931 185.9315 14.3 56 5 5
## 6 -1.948477866 28.00000 185.9315 14.9 66 5 6
## 7 -0.946873375 23.00000 299.0000 8.6 65 5 7
## 8 -2.668268458 19.00000 99.0000 13.8 59 5 8
## 9 -3.841328812 8.00000 19.0000 20.1 61 5 9
## 10 -0.678931468 42.12931 194.0000 8.6 69 5 10
## 11 -0.853351826 7.00000 185.9315 6.9 74 5 11
## 12 -1.166927803 16.00000 256.0000 9.7 69 5 12
## 13 -1.289318002 11.00000 290.0000 9.2 66 5 13
## 14 -1.396454514 14.00000 274.0000 10.9 68 5 14
## 15 -2.845105287 18.00000 65.0000 13.2 58 5 15
## 16 -1.567359423 14.00000 334.0000 11.5 64 5 16
## 17 -1.222394066 34.00000 307.0000 12.0 66 5 17
## 18 -3.825353390 6.00000 78.0000 18.4 57 5 18
## 19 -1.090564782 30.00000 322.0000 11.5 68 5 19
## 20 -2.386816909 11.00000 44.0000 9.7 62 5 20
## 21 -2.873187492 1.00000 8.0000 9.7 59 5 21
## 22 -1.872243506 11.00000 320.0000 16.6 73 5 22
## 23 -2.669232346 4.00000 25.0000 9.7 61 5 23
## 24 -2.261929720 32.00000 92.0000 12.0 61 5 24
## 25 -3.011581630 42.12931 66.0000 16.6 57 5 25
## 26 -2.158257917 42.12931 266.0000 14.9 58 5 26
## 27 -1.538704916 42.12931 185.9315 8.0 57 5 27
## 28 -2.344969618 23.00000 13.0000 12.0 67 5 28
## 29 -0.791727079 45.00000 252.0000 14.9 81 5 29
## 30 1.554210286 115.00000 223.0000 5.7 79 5 30
## 31 -0.187685699 37.00000 279.0000 7.4 76 5 31
## 32 0.439245831 42.12931 286.0000 8.6 78 6 1
## 33 0.042610950 42.12931 287.0000 9.7 74 6 2
## 34 -1.376032750 42.12931 242.0000 16.1 67 6 3
## 35 0.398014216 42.12931 186.0000 9.2 84 6 4
## 36 0.625241623 42.12931 220.0000 8.6 85 6 5
## 37 -0.382709097 42.12931 264.0000 14.3 79 6 6
## 38 -0.243569838 29.00000 127.0000 9.7 82 6 7
## 39 1.091866658 42.12931 273.0000 6.9 87 6 8
## 40 0.940311180 71.00000 291.0000 13.8 90 6 9
## 41 0.539027021 39.00000 323.0000 11.5 87 6 10
## 42 0.844370224 42.12931 259.0000 10.9 93 6 11
## 43 0.973972646 42.12931 250.0000 9.2 92 6 12
## 44 -0.138130610 23.00000 148.0000 8.0 82 6 13
## 45 -0.150332691 42.12931 332.0000 13.8 80 6 14
## 46 0.056581885 42.12931 322.0000 11.5 79 6 15
## 47 -1.309881650 21.00000 191.0000 14.9 77 6 16
## 48 -1.825083373 37.00000 284.0000 20.7 72 6 17
## 49 -1.757561977 20.00000 37.0000 9.2 65 6 18
## 50 -1.506802232 12.00000 120.0000 11.5 73 6 19
## 51 -1.108851924 13.00000 137.0000 10.3 76 6 20
## 52 0.066456323 42.12931 150.0000 6.3 77 6 21
## 53 0.347035588 42.12931 59.0000 1.7 76 6 22
## 54 0.040389232 42.12931 91.0000 4.6 76 6 23
## 55 0.260653773 42.12931 250.0000 6.3 76 6 24
## 56 -0.370109593 42.12931 135.0000 8.0 75 6 25
## 57 -0.223730573 42.12931 127.0000 8.0 78 6 26
## 58 -1.074802642 42.12931 47.0000 10.3 73 6 27
## 59 -0.677430608 42.12931 98.0000 11.5 80 6 28
## 60 -1.517455969 42.12931 31.0000 14.9 77 6 29
## 61 0.063923497 42.12931 138.0000 8.0 83 6 30
## 62 3.328157849 135.00000 269.0000 4.1 84 7 1
## 63 0.998494748 49.00000 248.0000 9.2 85 7 2
## 64 0.387921413 32.00000 236.0000 9.2 81 7 3
## 65 0.133283438 42.12931 101.0000 10.9 84 7 4
## 66 1.533394539 64.00000 175.0000 4.6 83 7 5
## 67 0.624451390 40.00000 314.0000 10.9 83 7 6
## 68 2.284041379 77.00000 276.0000 5.1 88 7 7
## 69 2.707948553 97.00000 267.0000 6.3 92 7 8
## 70 2.791203977 97.00000 272.0000 5.7 92 7 9
## 71 1.863509895 85.00000 175.0000 7.4 89 7 10
## 72 0.350209295 42.12931 139.0000 8.6 82 7 11
## 73 -1.216128376 10.00000 264.0000 14.3 73 7 12
## 74 -0.758859511 27.00000 175.0000 14.9 81 7 13
## 75 0.455192235 42.12931 291.0000 14.9 91 7 14
## 76 -1.508731178 7.00000 48.0000 14.3 80 7 15
## 77 0.921193571 48.00000 260.0000 6.9 81 7 16
## 78 0.308703236 35.00000 274.0000 10.3 82 7 17
## 79 1.478979323 61.00000 285.0000 6.3 84 7 18
## 80 1.868497283 79.00000 187.0000 5.1 87 7 19
## 81 0.671930832 63.00000 220.0000 11.5 85 7 20
## 82 -0.896618386 16.00000 7.0000 6.9 74 7 21
## 83 0.361230727 42.12931 258.0000 9.7 81 7 22
## 84 0.276323576 42.12931 295.0000 11.5 82 7 23
## 85 1.611355864 80.00000 294.0000 8.6 86 7 24
## 86 1.947742901 108.00000 223.0000 8.0 85 7 25
## 87 -0.408805186 20.00000 81.0000 8.6 82 7 26
## 88 -0.021779888 52.00000 82.0000 12.0 86 7 27
## 89 1.651113530 82.00000 213.0000 7.4 88 7 28
## 90 1.089261260 50.00000 275.0000 7.4 86 7 29
## 91 1.099930641 64.00000 253.0000 7.4 83 7 30
## 92 0.635157952 59.00000 254.0000 9.2 81 7 31
## 93 0.617531010 39.00000 83.0000 6.9 81 8 1
## 94 -1.057186052 9.00000 24.0000 13.8 81 8 2
## 95 0.133308250 16.00000 77.0000 7.4 82 8 3
## 96 1.923901262 78.00000 185.9315 6.9 86 8 4
## 97 0.967276604 35.00000 185.9315 7.4 85 8 5
## 98 2.040543791 66.00000 185.9315 4.6 87 8 6
## 99 3.494742295 122.00000 255.0000 4.0 89 8 7
## 100 1.998659486 89.00000 229.0000 10.3 90 8 8
## 101 2.630779572 110.00000 207.0000 8.0 90 8 9
## 102 1.411713677 42.12931 222.0000 8.6 92 8 10
## 103 0.405734151 42.12931 137.0000 11.5 86 8 11
## 104 0.588681342 44.00000 192.0000 11.5 86 8 12
## 105 0.265527196 28.00000 273.0000 11.5 82 8 13
## 106 0.743402150 65.00000 157.0000 9.7 80 8 14
## 107 -0.272386738 42.12931 64.0000 11.5 79 8 15
## 108 -0.606711599 22.00000 71.0000 10.3 77 8 16
## 109 0.683392121 59.00000 51.0000 6.3 79 8 17
## 110 -0.156103882 23.00000 115.0000 7.4 76 8 18
## 111 0.009759647 31.00000 244.0000 10.9 78 8 19
## 112 0.170089376 44.00000 190.0000 10.3 78 8 20
## 113 -0.835093025 21.00000 259.0000 15.5 77 8 21
## 114 -1.859351035 9.00000 36.0000 14.3 72 8 22
## 115 -0.200299233 42.12931 255.0000 12.6 75 8 23
## 116 0.347594848 45.00000 212.0000 9.7 79 8 24
## 117 3.714159713 168.00000 238.0000 3.4 81 8 25
## 118 1.515436281 73.00000 215.0000 8.0 86 8 26
## 119 1.165758626 42.12931 153.0000 5.7 88 8 27
## 120 1.950987993 76.00000 203.0000 9.7 97 8 28
## 121 3.610491595 118.00000 225.0000 2.3 94 8 29
## 122 2.572753754 84.00000 237.0000 6.3 96 8 30
## 123 2.318437419 85.00000 188.0000 6.3 94 8 31
## 124 2.755061274 96.00000 167.0000 6.9 91 9 1
## 125 2.788663526 78.00000 197.0000 5.1 92 9 2
## 126 3.009460969 73.00000 183.0000 2.8 93 9 3
## 127 3.117287527 91.00000 189.0000 4.6 93 9 4
## 128 1.261533459 47.00000 95.0000 7.4 87 9 5
## 129 -0.307407979 32.00000 92.0000 15.5 84 9 6
## 130 0.288385535 20.00000 252.0000 10.9 80 9 7
## 131 0.201381383 23.00000 220.0000 10.3 78 9 8
## 132 -0.080221684 21.00000 230.0000 10.9 75 9 9
## 133 0.089014756 24.00000 259.0000 9.7 73 9 10
## 134 0.178983355 44.00000 236.0000 14.9 81 9 11
## 135 -0.585218928 21.00000 259.0000 15.5 76 9 12
## 136 0.765973407 28.00000 238.0000 6.3 77 9 13
## 137 -1.201024755 9.00000 24.0000 10.9 71 9 14
## 138 -0.962526164 13.00000 112.0000 11.5 71 9 15
## 139 1.051529437 46.00000 237.0000 6.9 78 9 16
## 140 -1.115457340 18.00000 224.0000 13.8 67 9 17
## 141 -0.780154001 13.00000 27.0000 10.3 76 9 18
## 142 -0.455537846 24.00000 238.0000 10.3 68 9 19
## 143 0.425438756 16.00000 201.0000 8.0 82 9 20
## 144 -1.236119100 13.00000 238.0000 12.6 64 9 21
## 145 -0.827263876 23.00000 14.0000 9.2 71 9 22
## 146 0.225218117 36.00000 139.0000 10.3 81 9 23
## 147 -1.321014311 7.00000 49.0000 10.3 69 9 24
## 148 -2.486651208 14.00000 20.0000 16.6 63 9 25
## 149 0.024162409 30.00000 193.0000 6.9 70 9 26
## 150 -0.315078976 42.12931 145.0000 13.2 77 9 27
## 151 -0.996490368 14.00000 191.0000 14.3 75 9 28
## 152 -0.202553520 18.00000 131.0000 8.0 76 9 29
## 153 -0.860425544 20.00000 223.0000 11.5 68 9 30X<-cbind(pca$ind$coord[,1], pca$ind$coord[,2]) %>% set_colnames(c("PC1", "PC2"))
head(X)## PC1 PC2
## 1 -0.5697737 -1.5388946
## 2 -0.6628665 -0.9220601
## 3 -1.5357042 -1.2459632
## 4 -1.5359488 -2.4670249
## 5 -2.1908721 -1.6677619
## 6 -1.9484779 -1.5487626And you, how do you choice the number of factors kept from PCA?




Share this post
Twitter
Google+
Facebook
Reddit
LinkedIn
StumbleUpon
Pinterest
Email